1554. Forbidden strings

A string of letters A, B, C is forbidden if there are three consecutive letters from which one is A, one is B and one is C. For example, BAACAACCBAAA is forbidden, while AABBCCAABB is not.

How many such strings of length n are not forbidden?

Input. Each line contains one number n (1 ≤ n ≤ 30).

Output. For each input value of n print in a separate line the number of strings of length n are not forbidden.

Sample input	Sample output
2 3 4	9 21 51

SOLUTION

recurrent relation

Algorithm analysis

Let rep[i] contains the number of not forbidden strings of length i, which two last letters are equal. Let nonrep[i] contains the number of not forbidden strings of length i, which two last letters are different. The answer to the problem is the value rep[n] + nonrep[n].

Let us calculate the values of the cells directly:

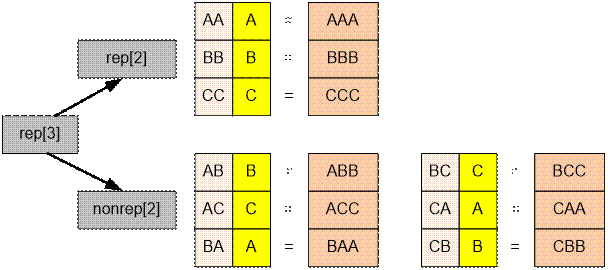
Computing the rep[i]. The i - th letter must be exactly the same as the letter at the (i – 1) - th place.

rep[i] = rep[i – 1] + nonrep[i – 1]

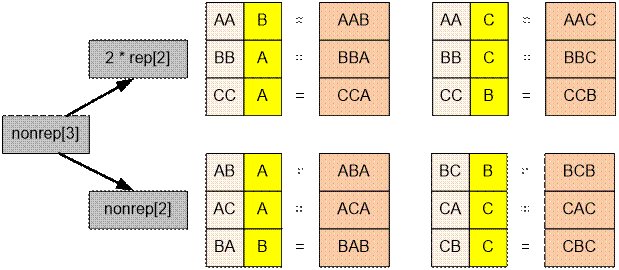
Computing the nonrep[i]. If the (i – 1) - th and (i – 2) - th letters are the same, we can place to the i - th position any of two letters that do not coincide with it. It the (i – 1) - th and (i – 2) - th letters are different, the (i – 1) - th letter to the i - th position can’t be duplicated, we can’t put to the i – th position the letter different from (i – 1) - th and (i – 2) - th (it is forbidden to put three consecutive letters in a row). Therefore in this case to the i – th position we must place the (i – 2) - th letter.

nonrep[i] = 2 * rep[i – 1] + nonrep[i – 1]

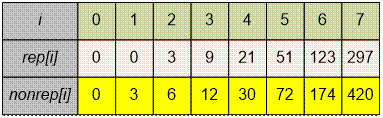
For example, the cells of the rep and nonrep arrays will contain the following values:

If we denote by rep(n) and nonrep(n) the functions that compute the number of not forbidden strings of length n, respectively, with repeated last two letters and not repeated, then we can write the recurrence relation:

,

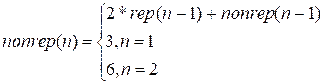
The answer is rep(n) + nonrep(n).

Algorithm realization

Declare the global arrays.

long long rep[31], nonrep[31];

Fill the cells of rep and nonrep arrays according to the formulas given above.

long long countNotForbidden(int n)

{

int i;

rep[1] = 0; rep[2] = 3;

nonrep[1] = 3; nonrep[2] = 6;

for(i = 3; i <= n; i++)

{

rep[i] = rep[i-1] + nonrep[i-1];

nonrep[i] = 2 * rep[i-1] + nonrep[i-1];

}

return rep[n] + nonrep[n];

}

The main part of the program.

while(scanf("%d",&n) == 1)

{

res = countNotForbidden(n);

printf("%lld\n",res);

}

Algorithm realization – recursion with memorization

#include <stdio.h>

#include <string.h>

int n;

long long repMem[31], nonrepMem[31];

long long nonrep(int n);

long long rep(int n)

{

if (n == 1) return 0;

if (n == 2) return 3;

if (repMem[n] != -1) return repMem[n];

return repMem[n] = rep(n - 1) + nonrep(n - 1);

}

long long nonrep(int n)

{

if (n == 1) return 3;

if (n == 2) return 6;

if (nonrepMem[n] != -1) return nonrepMem[n];

return nonrepMem[n] = 2 * rep(n - 1) + nonrep(n - 1);

}

int main(void)

{

memset(repMem,-1,sizeof(repMem));

memset(nonrepMem,-1,sizeof(nonrepMem));

while(scanf("%d",&n) == 1)

printf("%lld\n",rep(n) + nonrep(n));

return 0;

}

Java realization

import java.util.*;

public class Main

{

static int MAX = 31;

static long rep[] = new long[MAX], nonrep[] = new long[MAX];

static long countNotForbidden(int n)

{

rep[1] = 0; rep[2] = 3;

nonrep[1] = 3; nonrep[2] = 6;

for(int i = 3; i <= n; i++)

{

rep[i] = rep[i-1] + nonrep[i-1];

nonrep[i] = 2 * rep[i-1] + nonrep[i-1];

}

return rep[n] + nonrep[n];

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

while(con.hasNextInt())

{

int n = con.nextInt();

long res = countNotForbidden(n);

System.out.println(res);

}

}

}

Java realization – recursion with memorization

import java.util.*;

public class Main

{

static long repMem[] = new long[31];

static long nonrepMem[] = new long[31];

static long rep(int n)

{

if (n == 1) return 0;

if (n == 2) return 3;

if (repMem[n] != -1) return repMem[n];

return repMem[n] = rep(n - 1) + nonrep(n - 1);

}

static long nonrep(int n)

{

if (n == 1) return 3;

if (n == 2) return 6;

if (nonrepMem[n] != -1) return nonrepMem[n];

return nonrepMem[n] = 2 * rep(n - 1) + nonrep(n - 1);

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

Arrays.fill(repMem, -1);

Arrays.fill(nonrepMem, -1);

while(con.hasNext())

{

int n = con.nextInt();

System.out.println(rep(n) + nonrep(n));

}

con.close();

}

}